Segregation - Definitions and functions
This lab journal is created for the PhD project BIGSSS - Segregation and Polarization.
In this section we are defining Residential Segregation. We will program a custom Moran’s I function to be able to calculate the level of spatial auto-correlation.
Along the way, you will see some CSS trics, to perform computations in parallell.
1 Theory
- What is residential segregation intuitively?
- along which social dimensions?
- ethnic groups
- educational groups
- ethnic groups
- in which context?
- organizations
- social networks
- neighbourhoods
- organizations
- along which social dimensions?
- Type of segregation measures:
- non-spatial versus spatial
- zone-based or surface-based
- global versus local
- continuous social dimensions versus nominal social dimensions
- one or multiple groups per dimension
- one or more social dimensions
- Dimensions of segregation:
- evenness
- refers to the degree to which members of different groups are over- and underrepresented in different subareas relative to their overall proportions in the population.
- clustering
- refers to the proximity of subareas with similar group proportions to one another.
- exposure
- refers to the extent that members of one group are exposed to members of another group in their (local) environments.
- centralization
- concentration
- evenness
2 Assignment
A. Read the following papers:
- Reardon and O’Sullivan (2004)
- Yao et al. (2019)
- Hong, O’Sullivan, and Sadahiro (2014)
- Tivadar (2019)
B. For this BIGSSS we will use GIS data from Statistics Netherlands, at the municipality, district (‘wijk’), (‘buurt’) and 100-by-100 meter grid level. What are the basic requirements of data necessary and sufficient to determine the level of spatial segregation in specific areas of the Netherlands? Make a list of requirements for non-spatial and spatial measures.
C. How would you theoretically want to define the spatial distance between voters/citizens in the Netherlands?
D. Please formulate a precise definition of what you consider to be the relevant neighbourhood (or phrased otherwise ‘local environment’ or ‘social environment’) as inpunt for the segregation measures.
E. Which theoretical article on residential segregation should we definitely all read for this summer school? Please provide a reference and motivate your answer.
3 Measures of (spatial) Segregation
We cannot discuss all spatial segregation measures, we refer to:
3.1 Local environment
There are two important ingredients to spatial measures of segregation:
- the local environment
- the distance between local environments
Immediately a problem arises. What is our input data to construct the local environment? Is it surface-based or zone-based? During this workshop we will mostly rely on the spatial data of the highest resolution available to us, the 100-by-100 meter grid data. We could threat these as spatial units or as spatial points (the center of the raster cell), we could also use this type of aggregated data to construct a continuous population density surface in order to be able to apply surface-based measures.
Let us define the population density in the local environment of spatial unit \(i\) as:
\[\begin{equation} \tilde{\tau}_i = \Sigma_jw_{ij}\tau_j, \tag{3.1} \end{equation}\]
where \(w_{ij}\) is the (row-standardized!!) distance-based weight matrix (i.e. the spatial proximity between the associated point of the centroids of spatial units \(i\) and \(j\)) and \(\tau_j\) are the population densities at spatial unit \(j\).1 Naturally we could also calculate the population density in the local environment of spatial unit \(i\) per group \(k\).
\[\begin{equation} \tilde{\tau}^k_i = \Sigma_jw_{ij}\tau^k_j \tag{3.2} \end{equation}\]
And the spatial proportion of group \(k\) in the local environment of spatial unit/point \(i\) becomes:
\[\begin{equation} \tilde{\pi}^k_i = \frac{\tilde{\tau}^k_i}{\tilde{\tau}_i} \tag{3.3} \end{equation}\]
And these spatial proportions are important ingredients for our spatial measures of segregation.
Naturally, we need to define the weight matrix.
- Step 1: How are we going to measure the distance?
- Step 2: How should we deal with the distance of a point/unit to itself? Be aware that this depends on what you are calculating.
- Step 3: How are we going from a distance matrix to a weight matrix. In other words, what is our distance-decay function?
- Step 4: What about (row)standardization of the weight matrix??
3.2 Assignment
See the dataframe
popcountsand the weight matrixweightsbelow.popcountscontains the population density for two groups at 10 locations. Theweightsmatrix contains the proximity of these points, see (3.1). Based on these ingredients, construct the local environment of each location. That is, the spatial proportions (3.3)) with respect to these two groups at each location.
set.seed(567732)
g1 <- sample(20:400, 10) #counts group 1
g2 <- sample(20:400, 10) #counts group 2
popcounts <- data.frame(g1, g2)
distances <- matrix(sample(20:400, 100), nrow = 10, ncol = 10)
distances[lower.tri(distances)] <- (t(distances)[lower.tri(distances)])
weights <- exp(-distances/100)
diag(weights) <- 0
rm(list = c("g1", "g2", "distances"))
weights3.3 Exposure/Isolation index \(P^*\)
To demonstrate the use of the local environment, we are going to use the spatial exposure index. The spatial exposure index is computed as the average proportion of a group within the local environment of each member of another group. The spatial isolation of a group is simply the spatial exposure of a group to itself.
\(\tilde{\pi}^k_i\) is the spatial exposure to group \(k\) for people living in spatial unit \(i\). It is hence relatively straightforward to calculate the average exposure to group \(k=n\) for individuals with group membership \(k=m\). .
\[\begin{equation} \tilde{P}^*_{mn} = \frac{\Sigma_i \tau^m_i\tilde{\pi}^n_i}{\Sigma_i \tau^m_i} \tag{3.4} \end{equation}\]
Thus, \(\tilde{P}^*_{mn}\), is the average exposure to group \(n\) for members of group \(m\). Similarly, we can define: \(\tilde{P}^*_{nm}\) and \(\tilde{P}^*_{mm}\) (i.e. the isolation of group m) and \(\tilde{P}^*_{nn}\).
And if we have to average exposure of each group to the outgroup we can also define the average exposure to outgroup members.
3.4 Assignment
Please provide a conscise and clear formula for the spatial average exposure to outgroup members. Write the mathematic formula using in markdown.
3.5 Spatial correlation
Spatial correlation measures have not been addressed in the papers you read.
There are several forms
- Moran’s I
- Geary’s C
- Getis-Ord G
Moran’s I is given by:
\[\begin{equation} I= \gamma \Sigma_i\Sigma_jw_{ij}z_iz_j, \tag{3.5} \end{equation}\]
where \(w_{ij}\) is once again the distance-based weight matrix (i.e. the spatial proximity between the associated points) \(z_i\) and \(z_j\) are the scores (e.g.\(\tau^k\), or \(\pi^k\), or any other attribute) in deviations from the mean at point \(i\). And,
\[\begin{equation} 1/\gamma= S_0 * m_2 = \Sigma_i\Sigma_jw_{ij} * \frac{\Sigma_iz_i^2}{n}, \tag{3.5} \end{equation}\]
with: \(S_0 = \Sigma_i\Sigma_jw_{ij}\) and \(m_2 = \frac{\Sigma_iz_i^2}{n}\).
Thus \(S_0\) is the sum of the weight matrix and \(m_2\) is an estimate of the variance. For more information see (Anselin 1995).
Here also, some problems arise. Do we want a correlation between the count of members of a specific group in our spatial units, or between the proportion of a specific group. What we actually want to compare is whether a relatively high number of group k in a specific spatial point i correlates with the number of group m in the local environment of i. We then have two options:
- use a bivariate Moran’s I.
- calculate a mono-variate Moran’s I on proportions of group k, but correct for the population density.
Now that we provided some background on segregation measures, let us move on and see how we can implement these in R.
4 Getting started
4.1 Clean-up.
rm(list = ls())4.2 General custom functions
fpacage.check: Check if packages are installed (and install if not) in R (source).fsave: Function to save data with time stamp in correct directory
fsave <- function(x, file, location = "./data/processed/", ...) {
if (!dir.exists(location))
dir.create(location)
datename <- substr(gsub("[:-]", "", Sys.time()), 1, 8)
totalname <- paste(location, datename, file, sep = "")
print(paste("SAVED: ", totalname, sep = ""))
save(x, file = totalname)
}
fpackage.check <- function(packages) {
lapply(packages, FUN = function(x) {
if (!require(x, character.only = TRUE)) {
install.packages(x, dependencies = TRUE)
library(x, character.only = TRUE)
}
})
}
colorize <- function(x, color) {
sprintf("<span style='color: %s;'>%s</span>", color, x)
}4.3 Load necessary packages
packages = c("tidyverse", "rgl", "spdep", "geosphere", "truncnorm", "progress", "foreach", "doParallel",
"ape", "seg", "rgl", "OasisR", "compiler")
fpackage.check(packages)5 Moran’s I function
Let us make a function for Moran’s I. This function allows us to turn rowstandardization of the weight matrix on and off. We also adapted this version so we can calculate both the univariate and bivariate case.
5.1 Moran’s I.
# let us define a Moran's I function (heavily based on Moran.I of package ape) you can toggle
# rowstandardization
fMoranI <- function(x, y = NULL, weight, scaled = FALSE, na.rm = FALSE, alternative = "two.sided", rowstandardize = TRUE) {
if (is.null(y)) {
y <- x
}
if (dim(weight)[1] != dim(weight)[2])
stop("'weight' must be a square matrix")
nx <- length(x)
ny <- length(y)
if (dim(weight)[1] != nx | dim(weight)[1] != ny)
stop("'weight' must have as many rows as observations in 'x' (and 'y', for the bivariate case) ")
ei <- -1/(nx - 1)
nas <- is.na(x) | is.na(y)
if (any(nas)) {
if (na.rm) {
x <- x[!nas]
y <- y[!nas]
nx <- length(x)
weight <- weight[!nas, !nas]
} else {
warning("'x' and/or 'y' have missing values: maybe you wanted to set na.rm = TRUE?")
return(list(observed = NA, expected = ei, sd = NA, p.value = NA))
}
}
if (rowstandardize) {
ROWSUM <- rowSums(weight)
ROWSUM[ROWSUM == 0] <- 1
weight <- weight/ROWSUM
}
s <- sum(weight)
mx <- mean(x)
sx <- x - mx
my <- mean(y)
sy <- y - my
v <- sum(sx^2)
cv <- sum(weight * sx %o% sy)
obs <- (nx/s) * (cv/v)
cv_loc <- rowSums(weight * sx %o% sy)
obs_loc <- (nx/s) * (cv_loc/v)
if (scaled) {
i.max <- (nx/s) * (sd(rowSums(weight) * sx)/sqrt(v/(nx - 1)))
obs <- obs/i.max
obs_loc <- obs_loc/i.max
}
S1 <- 0.5 * sum((weight + t(weight))^2)
S2 <- sum((apply(weight, 1, sum) + apply(weight, 2, sum))^2)
s.sq <- s^2
k <- (sum(sx^4)/nx)/(v/nx)^2
sdi <- sqrt((nx * ((nx^2 - 3 * nx + 3) * S1 - nx * S2 + 3 * s.sq) - k * (nx * (nx - 1) * S1 - 2 *
nx * S2 + 6 * s.sq))/((nx - 1) * (nx - 2) * (nx - 3) * s.sq) - 1/((nx - 1)^2))
alternative <- match.arg(alternative, c("two.sided", "less", "greater"))
pv <- pnorm(obs, mean = ei, sd = sdi)
if (alternative == "two.sided")
pv <- if (obs <= ei)
2 * pv else 2 * (1 - pv)
if (alternative == "greater")
pv <- 1 - pv
list(observed = obs, expected = ei, sd = sdi, p.value = pv, observed_locals = obs_loc)
}
fMoranI <- cmpfun(fMoranI)5.2 Density corrected Moran’s I
Sometimes you may want to calculate a spatial correlation between attributes of spatial units that you want to weight by population density. For example, the proportion of ethnic minorities within a spatial unit or the level of polarization within a polling station, because these measures may be based on different population sizes. In the former case, you may want to revert to the count of ethnic minorities and another ethnic group and calculate a bivariate Moran’s I on these counts. In the latter case, such an approach is not feasible.
# Density corrected Moran's I.
fMoranIdens <- function(x, y = NULL, proxmat, dens = NULL, N = length(x)) {
# Adapted from Anselin (1995, eq. 7, 10, 11)
# https://onlinelibrary.wiley.com/doi/epdf/10.1111/j.1538-4632.1995.tb00338.x dens: the
# proportion of individuals in each cell over the district population if individual level data
# dens is.null and N is simply length of input if we have aggregate data then N should be total
# population size (or actually just a large number)
if (is.null(y)) {
y <- x
}
if (is.null(dens)) {
dens <- rep(1/N, times = N)
}
# correct scaling of opinions for densities #this is really inefficient, should use weighted
# var from hmsci
v1dens_ind <- rep(x, times = (dens * N))
v1dens <- (x - mean(v1dens_ind))/sd(v1dens_ind)
v2dens_ind <- rep(y, times = (dens * N))
v2dens <- (y - mean(v2dens_ind))/sd(v2dens_ind)
# (density) weighted proximity matrix
w <- proxmat
wdens <- t(dens * t(w))
wdens <- wdens/rowSums(wdens)
# density and proximity weighted locals
localI <- (v1dens * wdens %*% v2dens) #formula 7
# correct the normalization constants
m2 <- sum(v1dens^2 * dens)
S0 <- N #we know the weight matrix for the individual level should add up to N
ydens <- S0 * m2
globalI <- sum(localI * dens * N)/ydens # formula 10/11
return(list(globalI = globalI, localI = as.numeric(localI)))
}
fMoranIdens <- cmpfun(fMoranIdens)6 Toy data
We are going to simulate a lot of differently segregated worlds.
6.1 segregated world simulation function
This is a very old function I wrote ages ago. No need to understand.
# version 09-06-2007
# function define world
iniworld <- function(N = 2000, cn = 4, h = 1, tc = 0.9, pg = c(0.5, 0.5), distropTN = TRUE, plotworld = TRUE,
seed = NULL) {
# N= number of agents (even number) cn= number of clusters (even number) h= cluster homogeneity
# (0.5-1) tc= thinning constant. .9 means retain 90% pg= proportion of groups; length is number
# of groups distropTN= use truncated normal to generate opinions, default = false
# in paper opinions [0,1], here [-1,1] in paper tc is 1 - tc
if (is.null(seed))
seed <- sample(45667:159876, 1)
set.seed(seed)
N_ori <- N
# functions
spher_to_cart <- function(r, theta, phi) {
x = r * cos(phi) * sin(theta)
y = r * sin(theta) * sin(phi)
z = r * cos(theta)
coordinatesxyz <- matrix(c(x, y, z), ncol = 3)
return(coordinatesxyz)
}
distl <- function(x) {
distVincentySphere(x, matlonglat, r = 1)
}
# if tc<1 we need to increase initial N, make sure to keep even number
if (tc < 1) {
N <- trunc(N/(tc * 10)) * 10
}
# define (random) position of agents on sphere:
# http://mathworld.wolfram.com/SpherePointPicking.html
r <- 1
phi <- 2 * pi * runif(N)
theta <- acos(2 * runif(N) - 1)
coordinatesxyz <- spher_to_cart(r, theta, phi)
phi_r <- (360 * phi)/(2 * pi)
theta_r <- (180 * theta)/pi
lat <- 90 - theta_r
long <- ifelse(phi_r >= 0 & phi_r < 180, -phi_r, abs(phi_r - 360))
matlonglat <- matrix(c(long, lat), ncol = 2)
# improve: we only need to calculate half
matlonglatlist <- lapply(seq_len(nrow(matlonglat)), function(i) matlonglat[i, ])
distl <- function(x) {
distVincentySphere(x, matlonglat, r = 1)
}
matdist <- sapply(matlonglatlist, distl)
# model segregation: could be improved. check existing packages.
parents <- sample(1:N, cn)
groups <- rep(NA, N)
# fix if cn==1
groups[parents] <- sample(c(rep(1, round(cn * pg[1])), rep(-1, cn - round(cn * pg[1]))), cn, replace = FALSE)
# to whom do children belong
clusterchildren <- rep(NA, N)
for (i in c(1:N)) {
if (!(i %in% parents)) {
# which parents is closest
clusterchildren[i] <- parents[which(matdist[i, parents] == min(matdist[i, parents]))]
# give child same initial value as closest parent
group <- groups[clusterchildren[i]]
# change value child depending of cluster homogeneity
groups[i] <- ifelse(group == -1, sample(c(-1, 1), 1, prob = c(h, 1 - h)), sample(c(-1, 1),
1, prob = c(1 - h, h)))
}
}
# define opinions of agents
if (distropTN == TRUE) {
opinions <- rtruncnorm(N, a = -1, b = 1, mean = 0, sd = 0.45)
}
# if(distropTN==FALSE) {opinions <- runif(N, min = -1, max = 1)}
# for (future) plotting
color <- ifelse(groups == 1, "blue", "red")
# thin clusters, make cluster boundaries sharper
if (tc < 1) {
childIDi <- sampletc <- NA
# put in big function
for (i in 1:cn) {
childIDi <- which(clusterchildren == parents[i])
distchildparenti <- matdist[parents[i], childIDi]
# samplei <- sample(childIDi, trunc(tc*length(childIDi)),
# prob=exp(-distchildparenti)^2)
cutoffdistance <- quantile(distchildparenti, tc)
samplei <- childIDi[distchildparenti < cutoffdistance]
sampletc <- c(sampletc, samplei)
}
clusterchildren <- sampletc <- sampletc[-1]
sampletc <- c(sampletc, parents)
N_obs <- length(sampletc)
}
N <- N_ori #setting back to original input
if (tc == 1) {
sampletc <- NA
N_obs <- N_ori
}
if (plotworld & tc == 1) {
.check3d()
rgl.close()
plot3d(coordinatesxyz, col = color, box = FALSE, axes = FALSE, xlab = "", ylab = "", zlab = "",
size = 8, xlim = c(-1, 1), ylim = c(-1, 1), zlim = c(-1, 1))
rgl.spheres(0, 0, 0, radius = 0.995, color = "grey")
}
if (tc == 1) {
worldlist <- list(seed, coordinatesxyz, color, groups, opinions, matdist, N, cn, h, tc, pg, N_obs,
parents, clusterchildren, matlonglat)
names(worldlist) <- c("seed", "coordinatesxyz", "color", "groups", "opinions", "matdist", "N",
"cn", "h", "tc", "pg", "N_obs", "parents", "clusterchildren", "matlonglat")
return(worldlist)
}
if (plotworld & tc < 1) {
.check3d()
rgl.close()
plot3d(coordinatesxyz[sampletc, ], col = color[sampletc], box = FALSE, axes = FALSE, xlab = "",
ylab = "", zlab = "", size = 8, xlim = c(-1, 1), ylim = c(-1, 1), zlim = c(-1, 1))
rgl.spheres(0, 0, 0, radius = 0.995, color = "grey")
}
if (tc < 1) {
worldlist <- list(seed, coordinatesxyz[sampletc, ], color[sampletc], groups[sampletc], opinions[sampletc],
matdist[sampletc, sampletc], N, cn, h, tc, pg, N_obs, parents, clusterchildren, matlonglat[sampletc,
])
names(worldlist) <- c("seed", "coordinatesxyz", "color", "groups", "opinions", "matdist", "N",
"cn", "h", "tc", "pg", "N_obs", "parents", "clusterchildren", "matlonglat")
return(worldlist)
}
}6.2 Actual simulation of worlds
To generate our simulated worlds we used the following parameter-space:
- N= c(100, 200, 400, 800, 1600): number of agents (should be even number)
- cn= c(4,8,16,32,64): number of clusters (should be even number)
- h= c(0.6, 0.7, 0.8, 0.9, 1.0): cluster homogeneity (0.5-1)
- tc= c(0.6, 0.7, 0.8, 0.9, 1): thinning constant. .9 means retain 90%, the higher the thinning constant the more space between the seperate clusters.
- pg= c(0.5, 0.6, 0.7, 0.8, 0.9): proportion of group 1
# define parameters
N <- c(100, 200, 400, 800, 1600)
cn <- c(4, 8, 16, 32, 64)
h <- c(0.6, 0.7, 0.8, 0.9, 1)
tc <- c(0.6, 0.7, 0.8, 0.9, 1)
pg <- c(0.5, 0.6, 0.7, 0.8, 0.9)
# run the loop in parallel
n.cores <- parallel::detectCores() - 1 #save one core for other work
# create the cluster
my.cluster <- parallel::makeCluster(n.cores, type = "PSOCK")
# register it to be used by %dopar%
doParallel::registerDoParallel(cl = my.cluster)
# to get the same results
set.seed(5893743)
# make sure to define the correct folder beforehand
dataworlds <- foreach(Nsim = N, i = icount()) %:% foreach(cnsim = cn, j = icount()) %:% foreach(hsim = h,
k = icount()) %:% foreach(tcsim = tc, l = icount()) %:% foreach(pgsim = pg, m = icount(), .packages = packages,
.inorder = TRUE) %dopar% {
world <- iniworld(N = Nsim, cn = cnsim, h = hsim, tc = tcsim, pg = pgsim, plotworld = FALSE, seed = NULL)
save(world, file = paste("./data/processed/worlds/worldN", Nsim, "cn", cnsim, "h", hsim, "tc", tcsim,
"pg", pgsim, "rda", sep = ""), compress = "bzip2")
# return(test)
}6.3 Demonstrate measures on one world
N <- c(100, 200, 400, 800, 1600)
cn <- c(4, 8, 16, 32, 64)
h <- c(0.6, 0.7, 0.8, 0.9, 1)
tc <- c(0.6, 0.7, 0.8, 0.9, 1)
pg <- c(0.5, 0.6, 0.7, 0.8, 0.9)
load(paste("./data/processed/worlds/worldN", N[3], "cn", cn[3], "h", h[3], "tc", tc[3], "pg", pg[2],
"rda", sep = ""))
str(world)#> List of 15
#> $ seed : int 71865
#> $ coordinatesxyz : num [1:397, 1:3] 0.879 0.744 0.88 0.859 0.938 ...
#> $ color : chr [1:397] "red" "blue" "red" "red" ...
#> $ groups : num [1:397] -1 1 -1 -1 -1 -1 -1 -1 -1 -1 ...
#> $ opinions : num [1:397] -0.154 0.525 -0.203 0.791 -0.209 ...
#> $ matdist : num [1:397, 1:397] 0 0.424 0.335 0.345 0.153 ...
#> $ N : num 400
#> $ cn : num 16
#> $ h : num 0.8
#> $ tc : num 0.8
#> $ pg : num 0.6
#> $ N_obs : int 397
#> $ parents : int [1:16] 319 53 334 307 430 29 414 426 253 88 ...
#> $ clusterchildren: int [1:381] 48 60 62 118 131 136 190 252 294 309 ...
#> $ matlonglat : num [1:397, 1:2] 28.4 37.3 23.3 23 19.9 ...6.3.1 Plot this world
6.3.1.1 3d
plot <- {
plot3d(world$coordinatesxyz, col = world$color, box = FALSE, axes = FALSE, xlab = "", ylab = "",
zlab = "", size = 4, xlim = c(-1, 1), ylim = c(-1, 1), zlim = c(-1, 1))
rgl.spheres(0, 0, 0, radius = 0.99, color = "grey")
}6.3.1.2 projected
test <- world
# first define data.
mydf <- as.data.frame(cbind(as.numeric(test$groups == 1), as.numeric(test$groups == -1)))
# define the coordinates. (note: this are from a sphere)
mycoordinates <- test$matlonglat
mydf$Longitude <- test$matlonglat[, 1]
mydf$Latitude <- test$matlonglat[, 2]
points = st_as_sf(mydf, coords = c("Longitude", "Latitude"), crs = 4326)
graticule = st_graticule(lat = seq(-80, 80, 10), lon = seq(-180, 180, 10))
robinson = "+proj=robin +lon_0=0 +x_0=0 +y_0=0 +datum=WGS84 +units=m +no_defs"
projected = st_transform(points, robinson)
graticule = st_transform(graticule, robinson)
{
plot(projected$geometry, pch = 16, col = test$color, reset = FALSE)
plot(graticule$geometry, col = "#00000040", add = T)
}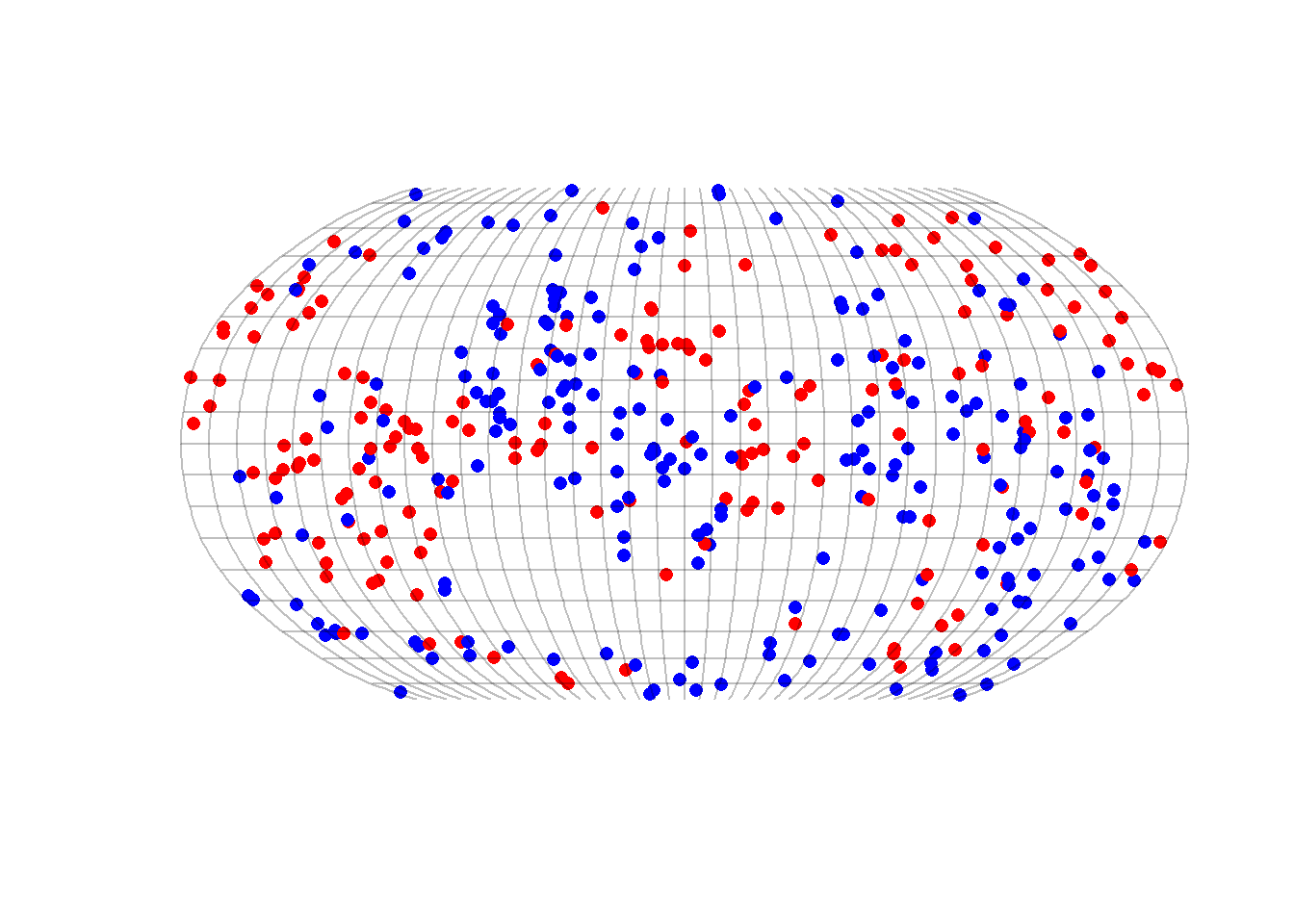
Figure 6.1: A world of reds and blues
What is your interpretation of this visual inspection? Is this world segregated or not? And at what scale?
6.3.2 retrieve data from simulated world
geodistances <- world$matdist
# we set distance to yourself to 0, be aware that in the weight matrix we may or may not want to
# set weight to yourself as 1.
diag(geodistances) <- 0
# retrieve the group membership
mydf <- as.data.frame(cbind(as.numeric(world$groups == 1), as.numeric(world$groups == -1)))
# define the coordinates
mycoordinates <- world$matlonglat6.3.3 setting the slope of the exponential distance decay function
Remember, the distance decay function is:
\[\begin{equation} w(d) = e^{-d*s} \tag{6.1} \end{equation}\]
s <- 16.3.4 segregation measures via package seg
Note that our coordinates are a sphere, package seg wants planar coordinates, to calculate distances. We will therefore provide distances ourselves to come to a local enviornment
geodistances <- world$matdist
diag(geodistances) <- 0
mygeodistances <- as.dist(geodistances) #the class of the distance matrix should be dist.
# explain!
myenv <- seg::localenv(x = mycoordinates, data = mydf, power = s, useExp = TRUE, scale = FALSE, maxdist = pi,
sprel = mygeodistances, tol = .Machine$double.eps)
segs <- spatseg(env = myenv, method = "all", useC = TRUE, negative.rm = FALSE, tol = .Machine$double.eps)
print("spatial dissimilarity")
segs@d #spatial dissimilarity
print("spatial relative diversity")
segs@r #spatial relative diversity
print("spatial information theory")
segs@h #spatial information theory
print("Spatial Isolation group 1")
segs@p[1, 1] #spatial exposure/isolation
print("Spatial Exposure group 1 to 2")
segs@p[1, 2]
print("Spatial Exposure group 2 to 1")
segs@p[2, 1]
print("Spatial Isolation group 2")
segs@p[2, 2]
# spatial proximity
sp <- isp(x = mycoordinates, data = mydf, nb = geodistances, fun = function(x) {
exp(-x * 1)
})
print("Spatial proximity")
sp#> [1] "spatial dissimilarity"
#> [1] 0.07473002
#> [1] "spatial relative diversity"
#> [1] 0.008463197
#> [1] "spatial information theory"
#> [1] 0.006155416
#> [1] "Spatial Isolation group 1"
#> [1] 0.5741968
#> [1] "Spatial Exposure group 1 to 2"
#> [1] 0.4258032
#> [1] "Spatial Exposure group 2 to 1"
#> [1] 0.5384847
#> [1] "Spatial Isolation group 2"
#> [1] 0.4615153
#> [1] "Spatial proximity"
#> [1] 1.026256.3.5 mean outgroup exposure
Eo <- mean(c(myenv@env[, 2][myenv@data[, 1] == 1], myenv@env[, 1][myenv@data[, 2] == 1]))
Eo#> [1] 0.47575776.3.6 Assignment
Please calculate White’s spatial proximity by hand (that is, via your own R code).
Only if you are stuch for more than an hour, click the
Codebutton on the right.
proximity <- exp(-geodistances * s)
diag(proximity) <- NA #let us not include the diagonal BE AWARE THAT IN OASISR YOU CANNOT DO THIS, SO VALUES ARE SLIGHTLY OFF.
mprox <- mean(proximity, na.rm = T) #mean proximity
# average proximity of members of group 1 / -1
mprox11 <- mean(proximity[world$groups == 1, world$groups == 1], na.rm = T)
mprox22 <- mean(proximity[world$groups == -1, world$groups == -1], na.rm = T)
pi1 <- sum(world$groups == 1)/length(world$groups)
pi2 <- sum(world$groups == -1)/length(world$groups)
# the actual formula
SP <- (pi1 * mprox11 + pi2 * mprox22)/mprox
SP6.3.7 Moran’s I
weights <- exp(-geodistances * s)
diag(weights) <- 0 #for Moran we do not want own location, because we are dealing with point data.
# let us interpret the group membership as an attribute of the point.
MIg <- fMoranI(world$groups, scaled = FALSE, weight = weights, na.rm = TRUE)
MIg$observed
# let us use count of group membership 1.
MIc1 <- fMoranI(myenv@data[, 1], scaled = FALSE, weight = weights, na.rm = TRUE)
MIc1$observed
# let us use count of group membership 2.
MIc2 <- fMoranI(myenv@data[, 2], scaled = FALSE, weight = weights, na.rm = TRUE)
MIc2$observed#> [1] 0.02639868
#> [1] 0.02639868
#> [1] 0.026398686.3.8 segregation measures via package OasisR
6.3.8.1 Spatial proximity
geodistances <- world$matdist
diag(geodistances) <- Inf
SP(x = mydf, d = geodistances, fdist = "e", beta = s)#> [1] 1.02636.3.8.2 Exposure
geodistances <- world$matdist
DPxy(x = mydf, d = geodistances, beta = s)#> [,1] [,2]
#> [1,] 0.5742 0.4258
#> [2,] 0.5385 0.46156.4 calculating segregtion measures of simulated worlds
This loop may take some time! You have to tweak it later in the assignment. Thus run only for a small part of the parameter-space.
# calculate different segregation indices for each world
N = c(100, 200, 400, 800, 1600)
cn = c(4, 8, 16, 32, 64)
h = c(0.6, 0.7, 0.8, 0.9, 1)
tc = c(0.6, 0.7, 0.8, 0.9, 1)
pg = c(0.5, 0.6, 0.7, 0.8, 0.9)
s = c(1, 2, 4, 8, 16)
# run the loop in parallel
n.cores <- parallel::detectCores() - 1
my.cluster <- parallel::makeCluster(n.cores, type = "PSOCK")
doParallel::registerDoParallel(cl = my.cluster)
# something goes wrong with N=100 h[5], pg[5] #yes all groups are same color , thus option
# .errorhandling = remove
dataworldsN1 <- foreach(Nsim = N, i = icount(), .combine = "rbind") %:% foreach(cnsim = cn, j = icount(),
.combine = "rbind") %:% foreach(hsim = h, k = icount(), .combine = "rbind") %:% foreach(tcsim = tc,
l = icount(), .combine = "rbind") %:% foreach(pgsim = pg, m = icount(), .combine = "rbind") %:% foreach(ssim = s,
.packages = packages, n = icount(), .combine = "rbind", .inorder = FALSE, .errorhandling = "remove") %dopar%
{
load(paste("./data/processed/worlds/worldN", Nsim, "cn", cnsim, "h", hsim, "tc", tcsim, "pg",
pgsim, "rda", sep = ""))
geodistances <- world$matdist
diag(geodistances) <- 0
mydf <- as.data.frame(cbind(as.numeric(world$groups == 1), as.numeric(world$groups == -1)))
mycoordinates <- world$matlonglat
geodistances <- world$matdist
diag(geodistances) <- 0
mygeodistances <- as.dist(geodistances) #the class of the distance matrix should be dist.
myenv <- seg::localenv(x = mycoordinates, data = mydf, power = ssim, useExp = TRUE, scale = FALSE,
maxdist = pi, sprel = mygeodistances, tol = .Machine$double.eps)
# PACKAGE SEG
segs <- spatseg(env = myenv, method = "all", useC = TRUE, negative.rm = FALSE, tol = .Machine$double.eps)
D <- segs@d
R <- segs@r
H <- segs@h
P_11 <- segs@p[1, 1]
P_12 <- segs@p[1, 2]
P_21 <- segs@p[2, 1]
P_22 <- segs@p[2, 2]
# Moran's I
weights <- exp(-geodistances * ssim)
diag(weights) <- 0 #for Moran we do not want own location.
MI <- fMoranI(world$groups, scaled = FALSE, weight = weights, na.rm = TRUE)$observed
# mean local exposure to outgroup ###not a segregation measure but useful in ABM###
Eo <- mean(c(myenv@env[, 2][myenv@data[, 1] == 1], myenv@env[, 1][myenv@data[, 2] == 1]))
# whites spatial proximity index
SP <- SP(x = mydf, d = geodistances, fdist = "e", beta = ssim)
id <- i * 10000 + j * 1000 + k * 100 + l * 10 + m
# SAVE IN DATAFRAME
data.frame(id = id, s = ssim, N = Nsim, cn = cnsim, h = hsim, tc = tcsim, pg = pgsim, seed = world$seed,
MI = MI, D = D, R = R, H = H, P_11 = P_11, P_12 = P_12, P_21 = P_21, P_22 = P_22, Eo = Eo,
SP = SP, i = i, j = j, k = k, l = l, m = m, n = n)
}6.5 Output
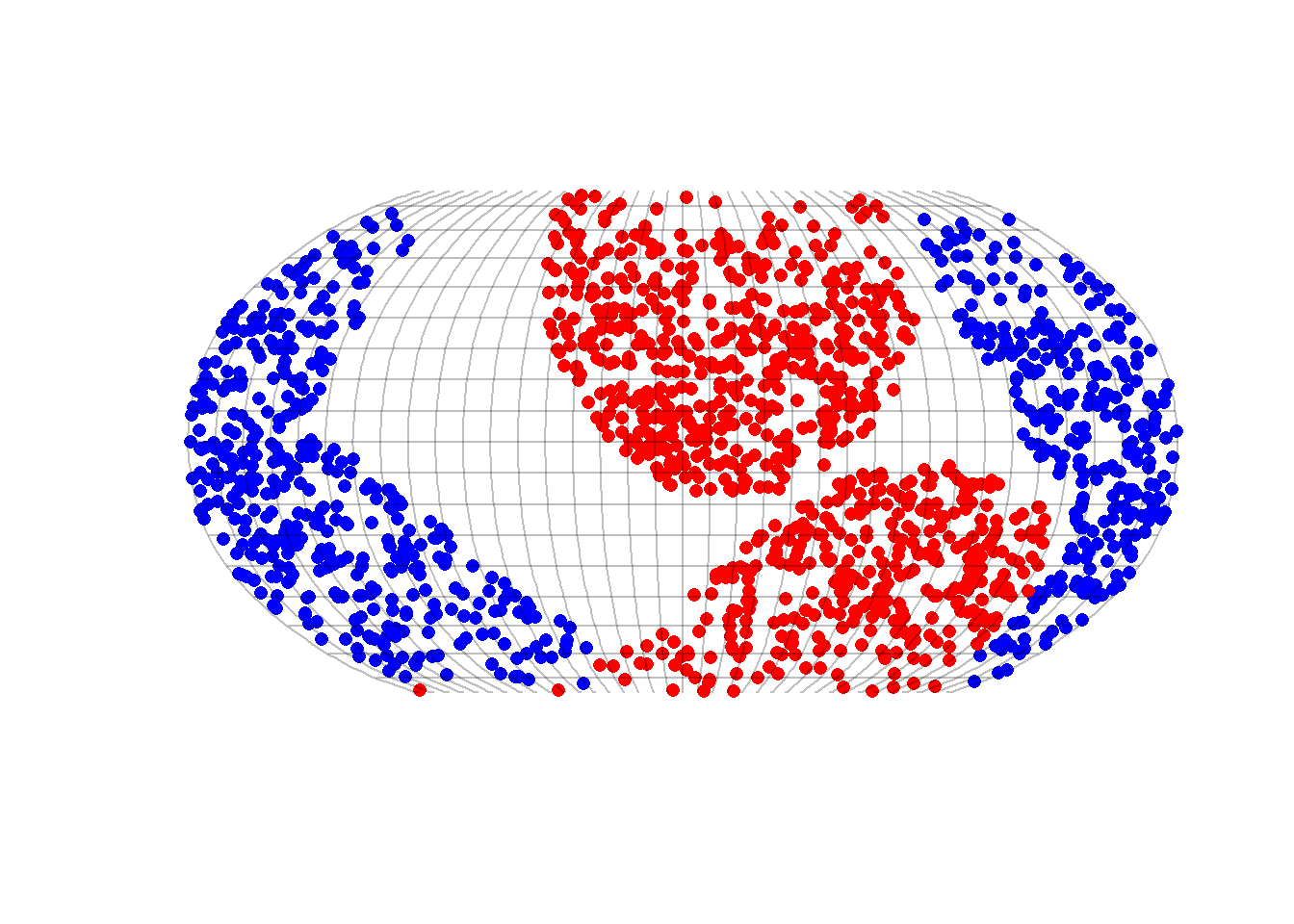
fsave(dataworldsN1, "SegWorlds")6.6 Plotting segregated worlds
load("./data/processed/20220629SegWorlds")
worlds <- x
rm(x)
require(tidyverse)
worlds %>%
filter(N == 1600) %>%
arrange(desc(H)) -> worldssel
load(paste("./data/processed/worlds/worldN", worldssel$N[1], "cn", worldssel$cn[1], "h", worldssel$h[1],
"tc", worldssel$tc[1], "pg", worldssel$pg[1], "rda", sep = ""))
world1 <- world{
plot3d(world1$coordinatesxyz, col = world1$color, box = FALSE, axes = FALSE, xlab = "", ylab = "",
zlab = "", size = 4, xlim = c(-1, 1), ylim = c(-1, 1), zlim = c(-1, 1))
rgl.spheres(0, 0, 0, radius = 0.99, color = "grey")
}test <- world1
# first define data.
mydf <- as.data.frame(cbind(as.numeric(test$groups == 1), as.numeric(test$groups == -1)))
# define the coordinates. (note: this are from a sphere)
mycoordinates <- test$matlonglat
mydf$Longitude <- test$matlonglat[, 1]
mydf$Latitude <- test$matlonglat[, 2]
points = st_as_sf(mydf, coords = c("Longitude", "Latitude"), crs = 4326)
graticule = st_graticule(lat = seq(-80, 80, 10), lon = seq(-180, 180, 10))
robinson = "+proj=robin +lon_0=0 +x_0=0 +y_0=0 +datum=WGS84 +units=m +no_defs"
projected = st_transform(points, robinson)
graticule = st_transform(graticule, robinson)
{
plot(projected$geometry, pch = 16, col = test$color, reset = FALSE)
plot(graticule$geometry, col = "#00000040", add = T)
}
References
You have to decide what you want to do when \(i=j\). Do you want to include your own spatial unit in the local environment of the unit? I would say yes.↩︎
Copyright © 2022 Jochem Tolsma / Thomas Feliciani / Rob Franken